FB_FirstOrderDigitalFilter

Description

This FB is defined to filter an Analog signal.

In any control system with an analog feedback signal present there is the risk of unwanted noise and jitter that can compromise the signal integrity yielding a less the desirable system.

This Kollmorgen UDFB"User Defined Function Block" UDFB can be used as a sub-function block in another program of the application. It is described using FBD, LD, ST or IL language. Input / output parameters of a UDFB (as well as private variables) are declared in the variable editor as local variables of the UDFB will provide a digital first order filter of an analog feedback signal from an LVDT, tension transducer, potentiometer, encoder, resolver, or some other like device. The amount of filtering is based on a gain value and can provide no filter to full filter conditioning.

The following figure shows the function block I/O

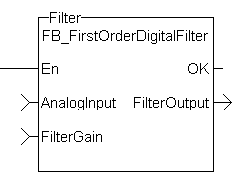
Figure 7-191: CBS First Order Digital Filter

Arguments

Inputs

EN	Description	Enables execution (FFLD only )
	Data type	BOOL
	Range	—
	Unit	n/a
	Default
AnalogInput	Description	Analog Input from transducer
	Data type	INT
	Range	—
	Unit	n/a
	Default
FilterGain	Description	Filter Gain
	Data type	REAL
	Range	[1 - 0.05]
	Unit	n/a
	Default	—

Outputs

OK	Description	Execution Complete
	Data type	BOOL
	Range	[0,1]
	Unit
FilterOutput	Description	Filtered analog input value
	Data type	REAL
	Range	[0,1]
	Unit

Usage

When using this UDFB, the Enable (EN) input should always be energized in order to provide the desired filtering.

• The AnalogInput input is the unfiltered “raw” analog feedback signal from an LVDT, tension transducer, potentiometer, or some other like device.
• The FilterGain defines the amount of filtering to be used. The range of the gain is from 1.0 or no filtering to 0.05 or the maximum filtering.
• The FilterOutput is the filtered analog input and is typically used as an input to some other function block or UDFB that has an analog input, for example the MCFB_GearedWebTension UDFB.
• The implementation of the digital first order filter is for PLCopenA vendor -and product- independent worldwide association active in Industrial Control and aiming at standardizing PLC file formats based on XML.
• The equation is defined as: Input*Gain+Output*(1-Gain) = Output
• The steady state filter delay with a gain of 0.8 can be seen in the following table.

FilterGain	FilterInput	FilterOutput
0.8	0	0
	100	80
	100	96
	100	99.2
	100	99.84
	100	99.968
	100	99.9936
	100	99.99872
	100	99.999744
	100	99.9999488
	100	99.99998976
	100	99.99999795
	100	99.99999959
	100	99.99999992
	100	99.99999998
	100	100
	100	100
	100	100
	100	100
	100	100
	100	100
	100	100
	100	100

Table 7-51: Filter Input Delay Example

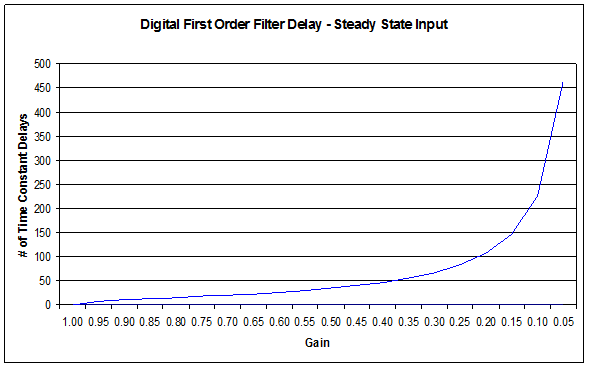
The range of the filter gain is between 1.00 and 0.05. From the table, for a filter gain of 0.8 there is a delay of 15 time constants with a time constant defined as the rate the UDFB is scanned or executed in the application. For example if the UDFB was executed every millisecond a gain of 0.8 would provide a filter delay of 15ms. Conversely a gain of 1.00 provides zero filtering and the output signal follows the input signal, and a gain of 0.05 provides the most filtering for 463 ms.

The numbers of filter delays for a steady state analog input at a given gain are shown in the table and graph below.

Gain	Filter Delay Tn
1.00	0
0.95	8
.90	11
.85	13
.80	15
.75	18
.70	20
.65	23
.60	26
.55	30
.50	35
.45	40
.40	47
.35	56
.30	66
.25	83
.20	107
.15	146
.10	226
.05	463

Of course a real world analog input is most always a varying feedback signal. In Table 2.3 this is shown with an initial input of 100, a gain of 0.8, and a random variability of 10%.Filter Input

Filter Input	Filter Current Output	Amount of Input Filtering	Random Filter % Variation
0	0	0	10%
100	80	-20
97.38903813	93.9112305	-3.477807626
92.67638093	92.92335084	0.246969915
94.12988912	93.88858146	-0.241307655
103.0835564	101.2445614	-1.838994993
91.16845433	93.18367575	2.015221422
93.23936976	93.22823096	-0.011138803
94.90272089	94.56782291	-0.334897986
103.3070737	101.5592235	-1.747850153
96.83149418	97.77704005	0.945545867
96.35024002	96.63560002	0.285360007
99.82417525	99.1864602	-0.637715045
105.0792636	103.9007029	-1.178560685
97.36988208	98.67604626	1.306164172
107.82502	105.9952253	-1.829794752
97.7886524	99.42996698	1.641314572
108.2038024	106.4490353	-1.754767081
91.58527607	94.55802792	2.972751845
93.6783421	93.85427926	0.175937164
102.8695349	101.0664838	-1.803051129
93.95916817	95.3806313	1.421463121
108.6579707	106.0025028	-2.655467871
109.3425748	108.6745604	-0.668014397
103.9066	104.8601921	0.953592077
92.30112142	94.81293555	2.511814127
109.4460726	106.5194452	-2.926627416
94.88799896	97.21428821	2.326289251
105.4738635	103.8219484	-1.651915057
102.988167	103.1549233	0.166756284
92.92925408	94.97438792	2.045133846
95.58185568	95.46036213	-0.121493552
109.414248	106.6234708	-2.790777178
106.5661311	106.577599	0.011467953
99.85857253	101.2023778	1.343805301
107.865421	106.5328124	-1.332608643
92.19683177	95.0640279	2.867196126
104.8558146	102.8974573	-1.958357346
104.5140236	104.1907104	-0.323313268
104.3675014	104.3321432	-0.035358206
109.2704266	108.2827699	-0.987656683
101.4962729	102.8535723	1.35729941
92.19199163	94.32430776	2.132316128
99.13065312	98.16938405	-0.961269073
103.5068114	102.4393259	-1.067485466
109.502983	108.0902516	-1.412731426
99.05504822	100.8620889	1.80704068
94.97711299	96.15410817	1.176995182
107.1063597	104.9159094	-2.190450308
91.12245188	93.88114339	2.758691504
108.130314	105.2804799	-2.849834129
104.2923832	104.4900025	0.197619344
101.3775072	102.0000062	0.62249907
100.5303014	100.0399168	-0.490384645	Averages

Table 7-52: Filter Input Lag Example - Random Input

Example

Structured Text

//Filter analog input signal with a gain of 0.8 to remove noise
FilteredOutput:= Inst_FB_FirstOrderDigitalFilter( AnalogInput1Value, 0.8 );

Ladder Diagram

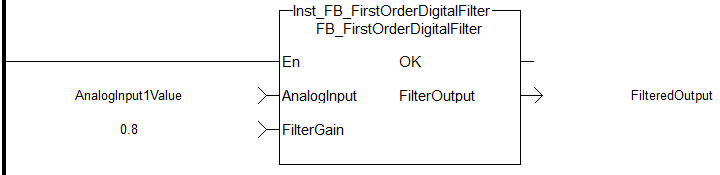
Function Block Diagram

 [Top]