This Kollmorgen UDFB
"User Defined Function Block"
UDFB can be used as a sub-function block in another program of the application. It is described using FBD, LD, ST or IL language. Input / output parameters of a UDFB (as well as private variables) are declared in the variable editor as local variables of the UDFB facilitates dancer and tension control in an electronic geared master/slave machine design. This is done by using the analog feedback from a LVDT, tension transducer, potentiometer, encoder, resolver or some other similar device. The analog feedback value is compared to a pre-determined analog set-point. The difference or error is used in a PID "Proportional-Integral-Derivative"
A PID controller is a generic control-loop feedback mechanism widely used in industrial control systems.
An "error" occurs when an event or a disturbance triggers off a change in the process variable.
A PID controller attempts to correct the error between a measured process variable and a desired setpoint by calculating and then outputting a corrective action that can adjust the process accordingly algorithm with the summed output driving changes to the master/slave gearing relationship. This results in the slave axis either speeding up or slowing down to maintain desired tension.
The following figure shows the function block I/O.
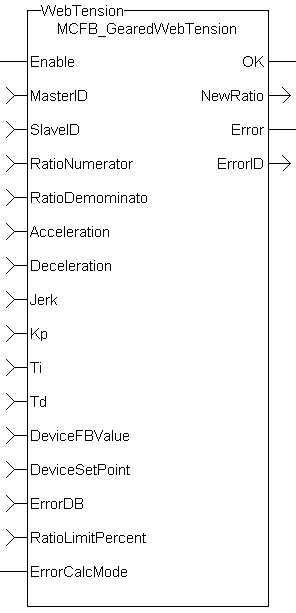
Figure 7-256: MCFB_GearedWebTension Function Block I/O
Arguments
Inputs
| Enable | Description | Enables execution |
| Data Type | BOOL | |
| Range | [0,1] | |
| Unit | N/A | |
| Default | - | |
| MasterID | Description | Identifies the master axis |
| Data Type | AXIS_REF | |
| Range | ||
| Unit | N/A | |
| Default | - | |
| SlaveID | Description | Identifies the slave axis |
| Data Type | AXIS_REF | |
| Range | ||
| Unit | N/A | |
| Default | - | |
| RatioNumerator | Description | Numerator of the master/slave ratio |
| Data Type | DINT | |
| Range | [-2147483648 to +2147483647] | |
| Unit | N/A | |
| Default | - | |
| RatioDenominator | Description | Denominator of the master/slave ratio |
| Data Type | DINT | |
| Range | [-2147483648 to +2147483647] | |
| Unit | N/A | |
| Default | - | |
| Acceleration | Description | Trapezoidal: acceleration rate, S-Curve: maximum acceleration |
| Data Type | LREAL | |
| Range | [-1.7E308 to 1.7E308 and -1.7E-308 to 1.7E-308 (14 to 15 significant digits of accuracy)] | |
| Unit | N/A | |
| Default | - | |
| Deceleration | Description | Trapezoidal: deceleration rate, S-Curve: not used |
| Data Type | LREAL | |
| Range | [-1.7E308 to 1.7E308 and -1.7E-308 to 1.7E-308 (14 to 15 significant digits of accuracy)] | |
| Unit | N/A | |
| Default | - | |
| Jerk In physics, jerk is the rate of change of acceleration; more precisely, the derivative of acceleration with respect to time
|
Description | Trapezoidal: 0, S-Curve: constant jerk In physics, jerk is the rate of change of acceleration; more precisely, the derivative of acceleration with respect to time |
| Data Type | LREAL | |
| Range | [-1.7E308 to 1.7E308 and -1.7E-308 to 1.7E-308 (14 to 15 significant digits of accuracy)] | |
| Unit | N/A | |
| Default | - | |
| Kp | Description | Proportional gain |
| Data Type | LREAL | |
| Range | [-1.7E308 to 1.7E308 and -1.7E-308 to 1.7E-308 (14 to 15 significant digits of accuracy)] | |
| Unit | N/A | |
| Default | - | |
| Ti | Description | Integral gain |
| Data Type | LREAL | |
| Range | [-1.7E308 to 1.7E308 and -1.7E-308 to 1.7E-308 (14 to 15 significant digits of accuracy)] | |
| Unit | N/A | |
| Default | - | |
| Td | Description | Derivative gain |
| Data Type | LREAL | |
| Range | [-1.7E308 to 1.7E308 and -1.7E-308 to 1.7E-308 (14 to 15 significant digits of accuracy)] | |
| Unit | N/A | |
| Default | - | |
| DeviceFBValue | Description | Analog input |
| Data Type | DINT | |
| Range | [-2147483648 to +2147483647] | |
| Unit | N/A | |
| Default | - | |
| DeviceSetPoint | Description | Analog set point |
| Data Type | DINT | |
| Range | [-2147483648 to +2147483647] | |
| Unit | N/A | |
| Default | - | |
| ErrorDB | Description | Maximum or minimum error between DeviceFBValue and DeviceSetPoint before a change will take place. |
| Data Type | LREAL | |
| Range | [-1.7E308 to 1.7E308 and -1.7E-308 to 1.7E-308 (14 to 15 significant digits of accuracy)] | |
| Unit | N/A | |
| Default | - | |
| RatioLimitPercent | Description | Maximum and minimum master/slave ratio window |
| Data Type | LREAL | |
| Range | [-1.7E308 to 1.7E308 and -1.7E-308 to 1.7E-308 (14 to 15 significant digits of accuracy)] | |
| Unit | N/A | |
| Default | - | |
| ErrorCalcMode | Description | Not set: DeviceFBValue-DeviceSetPoint, Set: DeviceSetPoint-DeviceFBValue |
| Data Type | BOOL | |
| Range | [0,1] | |
| Unit | N/A | |
| Default | - |
Output
| OK | Description | The output will have power flow after the enable input has been energized. |
| Data Type | BOOL | |
| Range | [0,1] | |
| Unit | N/A | |
| NewRatio | Description | New master/slave ratio |
| Data Type | REAL | |
| Range | [-3.4E38 to 3.4E38 and -3.4E-38 to 3.4E-38 (6 to 7 significant digits of accuracy)] | |
| Unit | N/A | |
| Error | Description | Function A function calculates a result according to the current value of its inputs. A function has no internal data and is not linked to declared instances. block error |
| Data Type | BOOL | |
| Range | [0,1] | |
| Unit | N/A | |
| ErrorID | Description | Function block error value |
| Data Type | INT | |
| Range | [-32768 to +32767] | |
| Unit | N/A |
Usage
This Kollmorgen UDFB is used in conjunction with the main ladder MC_GearIn function and it is assumed that the master/slave move is active. Internal to the Kollmorgen UDFB is another call to the MC_GearIn function therefore the MasterID, SlaveID, RatioNumerator, RatioDenominator, Acceleration, Deceleration, and Jerk inputs are the same values as the main ladder MC_GearIn function input values, both with the Buffer input of 0. This assures that the initial starting master/slave ratio will transition to the new Kollmorgen UDFB ratio smoothly.
This Kollmorgen UDFB will change the master/slave ratio that was defined by the MC_GearIn function based on the error between the analog input and the analog set-point. The magnitude of the ratio and the rate of the ratio change is defined by the Kp, Ti, Td PID gain values. The new ratio calculated is output at the NewRatio output.
The RatioLimitPercent input is the maximum and minimum theoretical new ratio that can be changed. This provides a +/- window limit around the running ratio to prevent unwanted motion in the event of a web break or analog feedback failure.
Example 1
-
-
This example assumes that the analog feedback device
A process whereby some proportion of the output signal of a system is passed (fed back) to the input.
In automation, a device coupled to each motor to provide indication of the motor's shaft angle, for use in commutating the motor and controlling its speed and position is located after (or downstream in the process) the feedroll axis.
RatioNumerator = 1
RatioDemominator = 2 Therefore the master/slave starting ratio is 0.5000000
ErrorCaclMode = 0
DeviceFBValue = 6
DeviceSetPoint = 4 Therefore error 6 – 4 = 2
Kp = 0.005
Ti = 0
Td= 0
From the equation:
New RatioDemominator = (RatioDemoninator - Kp * error)
Therefore the new RatioDenominator = (2 - 0.005*2) = 1.99
Thus the new master/slave running ratio is 1 / 1.99 = 0.502512562
Since the master/slave ratio is greater that the previous ration the slave axis is going faster and the tension is reduced.
Example 2
-
-
This example assumes that the analog feedback device is located before (or upstream in the process) the feedroll axis.
This is the same example as example 1 with the exception of the ErrorCaclMode input Boolean set.
RatioNumerator = 1
RatioDemominator = 2 Therefore the master/slave starting ratio is 0.5000000
ErrorCaclMode = 1
DeviceFBValue = 6
DeviceSetPoint = 4 Therefore error is 4 – 6 = -2
Kp = 0.005
Ti = 0
Td= 0
From the equation:
New RatioDemominator = (RatioDemoninator – (Kp * error))
Therefore the new RatioDenominator = (2 + 0.005*2) = 2.01
Thus the new master/slave running ratio is 1 / 2.01 = 0.497512437
Since the master/slave ratio is less than the previous ratio the slave axis is going slower and the tension is reduced.
PID Function in KAS:
There is a PID function in KAS that could be used for the PID control section in the Kollmorgen UDFB.
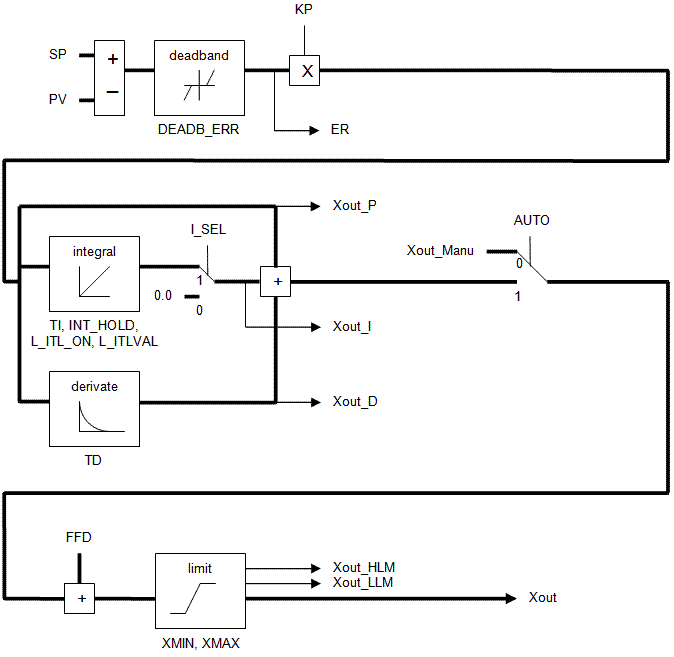
Programming tips:
The First Order Digital Filter Kollmorgen UDFB can be used to decrease excess dither on the analog input. The filtered analog value is then used at the DeviceFBValue input of the MCFB_GearedWebTension Kollmorgen UDFB .
The assumption is a MC_GearIn function block is first called in the main ladder and these initial values are then used at the inputs for the Kollmorgen UDFB. The resolution of the initial MC_GearIn the RatioNumerator and RatioDenominator inputs are directly related to the resolution of the calculated master/slave ratio (from the Kollmorgen UDFB inputs) and may need to be scaled accordingly.
Example 1
No scaling
Initial MC_GearIn input RatioNumerator = 2
Initial MC_GearIn input RatioDenominator = 1 then initial Master/Slave ratio = 2
Kollmorgen UDFB input RatioNumerator = 2
Kollmorgen UDFB input RatioDenominator = 1 then Kollmorgen UDFB Master/Slave ratio = 2
Kollmorgen UDFB input DeviceFBValue = 4
Kollmorgen UDFB input DeviceFBSetpoint = 3 then Device PID error = 1 assume KP = 1, Ti and Td =0
New Kollmorgen UDFB RatioNumerator = Current RatioNumerator – PID error = 2 – 1 = 1 then new Kollmorgen UDFB Master/Slave ratio = 1
Resolution = Master/Slave ratio:PID Error ratio = 1:1
The resolution is so coarse that a change of 1 for the error output of the PID creates a Master/Slave ratio change of 1. This results is a significant change to the slave velocity that will probably cause excess slack or web breakage.
Example 2
Scaling value = 1000
Initial MC_GearIn input RatioNumerator = 2
Initial MC_GearIn input RatioDenominator = 1 then initial Master/Slave ratio = 2
Kollmorgen UDFB input RatioNumerator = 2000
Kollmorgen UDFB input RatioDenominator = 1000 then Kollmorgen UDFB Master/Slave ratio = 2
Kollmorgen UDFB input DeviceFBValue = 4
Kollmorgen UDFB input DeviceFBSetpoint = 3 then Device PID error = 1 assume KP = 1, Ti and Td =0
New Kollmorgen UDFB RatioNumerator = Current RatioNumerator – PID error = 2000– 1 =1999 then new Kollmorgen UDFB Master/Slave ratio = 1999
Resolution = Master/Slave ratio:PID Error ratio = 2000:1
This resolution is much finer than example 1 so for a change of 1 for the error output of the PID this creates a Master/Slave ratio change of 1999. This results is a slower rate of change to the slave velocity that the more suited to good tension in a machine process.
Related Functions
Example
Ladder Example
Function Block Diagram Example
Structured Text Example
[Top]
