Arc-to-Arc Transitions
In arc-to-arc transition mode the transitions are handled as follows.
- The arc with the larger radius is shortened by an arc length equal to the corner distance.
- Using this point, a transition move is calculated such that it is tangent to both arcs.
- The arc with the smaller radius is shortened to the point where it is tangent with the transition move.
The transition move that connects the two original arcs derives its velocity from the velocity transition parameter and the acceleration and deceleration values are derived from the next move.
There are six special cases for Arc-to-Arc transitions.
| Transition Type | Description |
|---|---|
| Zero-distance Transitions | A zero-distance transition move is inserted when the corner distance is zero, which will only affect blending.
The path velocity will go to zero if the buffer mode is "Buffered". All other buffer modes may cause a large acceleration and jerk |
| Intersection Transitions | This will occur when the arcs intersect at two locations and the corner distance is equal to the arc length between the two intersections on the larger arc. The transition move will be zero distance.
The path velocity will go to zero if the buffer mode is "Buffered". All other buffer modes may cause a large acceleration and jerk. |
| Tangent Transitions with Opposite Direction |
A portion of the arc with the larger radius will be replaced by an arc whose length is equal to the corner distance. This will not affect the path, but will affect blending. If the arcs have the same radius, the incoming arc will be treated as having a larger radius. |
| Line Segment Transitions | For certain values of corner distance, the transition arc has an infinite radius and a line segment is used instead. |
| Same Circle, Same Direction Transitions | A transition arc with a length of twice the corner distance will be added if both arcs lie on the same circle and are in the same direction. This will not affect the path, but will affect blending. |
| Same Circle, Opposite Direction Transitions | The arcs will be shorted by an arc length equal to the corner distance and a zero distance transition will be inserted if both arcs lie on the same circle and are in the opposite direction. The path velocity will go to zero if the buffer mode is "Buffered". All other buffer modes may cause a large acceleration and jerk. |
| Case | Motion Path - Line-toArc / Arc-to-Line | Key | Motion Velocity Profile |
|---|---|---|---|
|
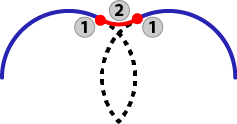
n-degree, arcs in opposite direction |
|
Blue: Incoming and outgoing circular motion Black: "Trimmed" path Red: Transition arc 1: Start / endpoint of arc move |

|
|
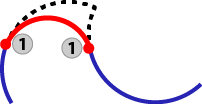
n-degree, arcs in same direction |
|
Blue: Incoming and outgoing circular motion Black: "Trimmed" path Red: Transition arc 1: Start / endpoint of arc move 2: Corner distance |

|
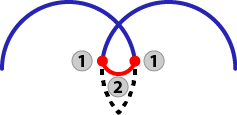
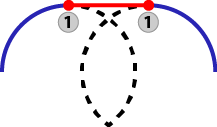
| Zero-distance |
|
Blue: Incoming and outgoing circular motion 1: Original Start / Endpoint of arc move |
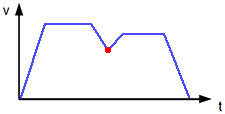
user units/sec |
| Intersection |
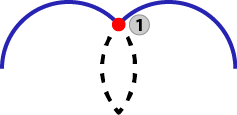
|
Blue: Incoming and outgoing circular motion Black: "Trimmed" path 1: Intersection of the two arcs |
|
| Tangent arcs, opposite direction |
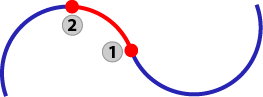
|
Blue: Incoming and outgoing circular motion Red: Transition arc 1: Original start / end point of moves 2: Start / Endpoint of arc move |

|
| Line segment |
|
Blue: Incoming and outgoing circular motion Red: Line Segment 1: Start / Endpoint of transition move |

|
| Same circle, same direction |

|
Blue: Incoming and outgoing circular motion Red: Transition arc 1: Start / Endpoint of arc move 2: Original start/end point |

|
| Same circle, opposite direction |
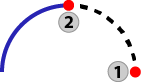
|
Blue: Incoming and outgoing circular motion 1: Original Start / Endpoint of arc move 2: Start / Endpoint of arc move |

|